When there is a need to make sequential code concurrent, there are two major options. First one is to take the original code as is, divide it between multiple executors, protect a mutable state from concurrent access, do all other "please don’t fail" multithreading stuff and hope for better. The alternative is to look through different concurrency concepts like data parallelism, actors, dataflows, CSP, etc., select the most appropriate one for your problem statement and write the solution on its basis. Luckily there is a library that provides DSLs for all major concurrency concepts called GPars. In this article I will tease how it can be used before my JEEConf talk.
Example problem
For demonstration purposes let’s take a problem of finding prime numbers and well-known algorithm to solve this problem - Sieve of Eratosthenes.
Just to remind it ourselves - a prime number is a natural number that has exactly two distinct natural number divisors: 1 and itself.
Sieve of Eratosthenes suggests that primes can be found with the following algorithm:
-
Create a list of consecutive integers from 2 through n: (2, 3, 4, …, n).
-
Take the smallest number from the list - it is prime.
-
Iterate through the list of remaining numbers and keep only those that can’t be divided by number found in previous step (that’s why it’s called sieve).
-
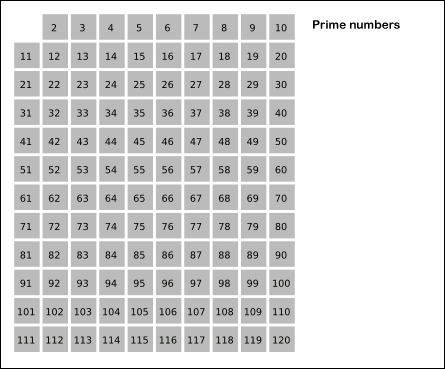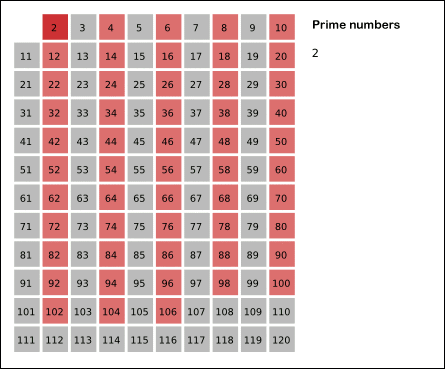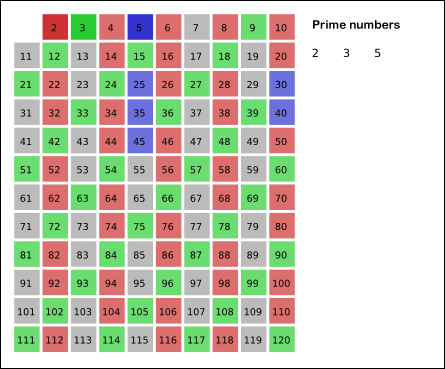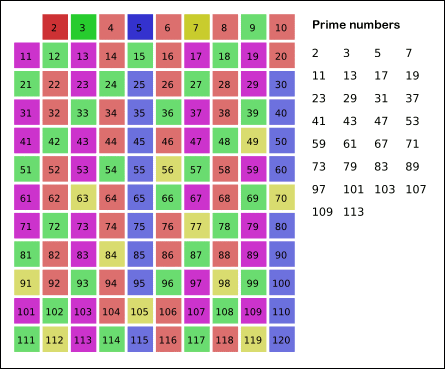
Repeat previous two steps until the desired number of primes is generated.
Sequential solution
Optimized sequential solution may look like following:
Turning this code into concurrent solution may become a challenge. Especially, turning into bug-free one. But even if it’s not a challenge for an experienced developer, if we check original algorithm description, we can find that there are concurrency concepts that fit it much more naturally that trivial migration from sequential to the concurrent solution.
Meet GPars
That’s when GPars comes into the game. First of all, add it to your project as following dependency:
Now let’s go through original algorithm step by step and implement it using the most powerful GPars concept - dataflows:
-
Create a list of consecutive integers from 2 through n: (2, 3, 4, …, n).
This one can easily be translated into asynchronous task:
-
Take the smallest number from the list - it is prime.
Again, it’s trivial:
-
Iterate through the list of remaining numbers and keep only those that can’t be divided by number found in the previous step.
Here, we define the asynchronous operator, that takes each number from remainingNumbers queue and push it into sievedNumbers queue if it can’t be divided by the number found in the previous step.
-
Repeat previous two steps until the desired number of primes is generated.
Complete code looks like following:
Conclusion
I can see several immediate benefits from choosing GPars Dataflows as a basic concept for implementing Sieve of Eratosthenes:
-
source code almost 100% matches original algorithm text script
-
zero lines of excessive concurrency infrastructure in the source code
-
safe and reliable execution in the concurrent environment provided by framework out-of-the-box